In this example we demonstrate how to run a time-domain simulation for a simple ThinCurr model of a cylinder.
- Note
- Running this example requires the h5py and pyvista python packages, which are installable using
pipor other standard methods.
Load ThinCurr library
To load the ThinCurr python module we need to tell python where to the module is located. This can be done either through the PYTHONPATH environment variable or within a script using sys.path.append() as below, where we look for the environement variable OFT_ROOTPATH to provide the path to where the OpenFUSIONToolkit is installed (/Applications/OFT for binaries on macOS).
Setup ThinCurr model
We now create a OFT_env instance for execution using two threads and a ThinCurr instance that utilizes that execution environment.
Once created, we setup the model from an existing HDF5 and XML mesh definition using setup_model(). For this model we have defined current jumpers using additional nodesets, which must be identified using the jumper_start argument (see ThinCurr Python Example: Time-domain simulation of a cylinder with jumpers for more information).
Finally, we initialize I/O for this model using setup_io() to enable output of plotting files for 3D visualization in VisIt, Paraview, or using pyvista below.
#----------------------------------------------
Open FUSION Toolkit Initialized
Development branch: v1_beta6
Revision id: 681e857
Parallelization Info:
# of MPI tasks = 1
# of NUMA nodes = 1
# of OpenMP threads = 2
Fortran input file = /var/folders/52/n5qxh27n4w19qxzqygz2btbw0000gn/T/oft_64866/oftpyin
XML input file = none
Integer Precisions = 4 8
Float Precisions = 4 8 16
Complex Precisions = 4 8
LA backend = native
#----------------------------------------------
Creating thin-wall model
Orientation depth = 895
Loading V(t) driver coils
Loading I(t) driver coils
# of points = 795
# of edges = 2259
# of cells = 1464
# of holes = 1
# of Vcoils = 0
# of closures = 0
# of Icoils = 1
Building holes
Loading region resistivity:
1 1.2570E-05
Define flux loop sensors
To visualize the results we define two circular flux loops at R=0.9 m, just inside the cylinder. While every sensor in ThinCurr is a flux loop, helper classes for defining specific types of common sensors (eg. circular loop or Mirnovs) are available in OpenFUSIONToolkit.ThinCurr.sensor, which also contains the save_sensors() function for saving this information to a ThinCurr-compatible file format.
After defining the sensors we use compute_Msensor() to setup the sensors and compute mutual matrices between the sensors and the model (Msensor) and the sensors and Icoils (Msc).
Loading floop information:
# of floops = 2
Setting jumper information:
1 -4.981645644143631E-02 -9.987583895355365E-01 -0.000000000000000E+00
Building element->sensor inductance matrix
Building coil->sensor inductance matrix
Compute self-inductance and resistivity matrices
With the model setup, we can now compute the self-inductance and resistivity matrices. A numpy version of the self-inductance matrix will be stored at tw_plate.Lmat. By default the resistivity matrix is not moved to python as it is sparse and converting to dense representation would require an increase in memory. These matrices correspond to the \(\textrm{L}\) and \(\textrm{R}\) matrices for the physical system
\(\textrm{L} \frac{\partial I}{\partial t} + \textrm{R} I = V\)
- Note
- For larger models calculating the self-inductance may take some time due to the \(N^2\) interaction of the elements (see ThinCurr Python Example: Using HODLR approximation for more information).
Building coil<->element inductance matrices
Time = 0s
Building coil<->coil inductance matrix
Building element<->element self inductance matrix
Time = 1s
Building resistivity matrix
Run time-domain simulation
With the model fully defined we can now use run_td() to perform a time-domain simulation. In this case we simulate 80 ms using a timestep of 0.2 ms (400 steps). We also specify using a direct solver for the time-advance (direct=True) and set the current in the single I-coil defined in the XML input file as a function of time (coil_currs), where the first column specifies time points in ascending order and the remaining columns specify coil currents at each time point.
Starting simulation Starting factorization Inverting real matrix Time = 1.2482999999999999E-002 Timestep 10 2.00000009E-03 1.49562419E-03 1 Timestep 20 4.00000019E-03 2.79602758E-03 1 Timestep 30 6.00000005E-03 3.89465247E-03 1 Timestep 40 8.00000038E-03 4.82152170E-03 1 Timestep 50 9.99999978E-03 5.60256978E-03 1 Timestep 60 1.20000001E-02 6.26014406E-03 1 Timestep 70 1.40000004E-02 6.81339065E-03 1 Timestep 80 1.60000008E-02 7.27862632E-03 1 Timestep 90 1.79999992E-02 7.66970450E-03 1 Timestep 100 1.99999996E-02 7.95727130E-03 1 Timestep 110 2.19999999E-02 6.74794754E-03 1 Timestep 120 2.40000002E-02 5.68625843E-03 1 Timestep 130 2.60000005E-02 4.78725182E-03 1 Timestep 140 2.80000009E-02 4.02759062E-03 1 Timestep 150 2.99999993E-02 3.38673173E-03 1 Timestep 160 3.20000015E-02 2.84675742E-03 1 Timestep 170 3.40000018E-02 2.39219540E-03 1 Timestep 180 3.59999985E-02 2.00978830E-03 1 Timestep 190 3.79999988E-02 1.68824021E-03 1 Timestep 200 3.99999991E-02 1.41796435E-03 1 Timestep 210 4.19999994E-02 1.19084760E-03 1 Timestep 220 4.39999998E-02 1.00003765E-03 1 Timestep 230 4.60000001E-02 8.39755870E-04 1 Timestep 240 4.80000004E-02 7.05134124E-04 1 Timestep 250 5.00000007E-02 5.92074881E-04 1 Timestep 260 5.20000011E-02 4.97131085E-04 1 Timestep 270 5.40000014E-02 4.17404401E-04 1 Timestep 280 5.60000017E-02 3.50458722E-04 1 Timestep 290 5.79999983E-02 2.94246915E-04 1 Timestep 300 5.99999987E-02 2.47049087E-04 1 Timestep 310 6.19999990E-02 2.07420511E-04 1 Timestep 320 6.40000030E-02 1.74147775E-04 1 Timestep 330 6.59999996E-02 1.46211823E-04 1 Timestep 340 6.80000037E-02 1.22756857E-04 1 Timestep 350 7.00000003E-02 1.03064231E-04 1 Timestep 360 7.19999969E-02 8.65305410E-05 1 Timestep 370 7.40000010E-02 7.26491053E-05 1 Timestep 380 7.59999976E-02 6.09944909E-05 1 Timestep 390 7.80000016E-02 5.12095066E-05 1 Timestep 400 7.99999982E-02 4.29942374E-05 1
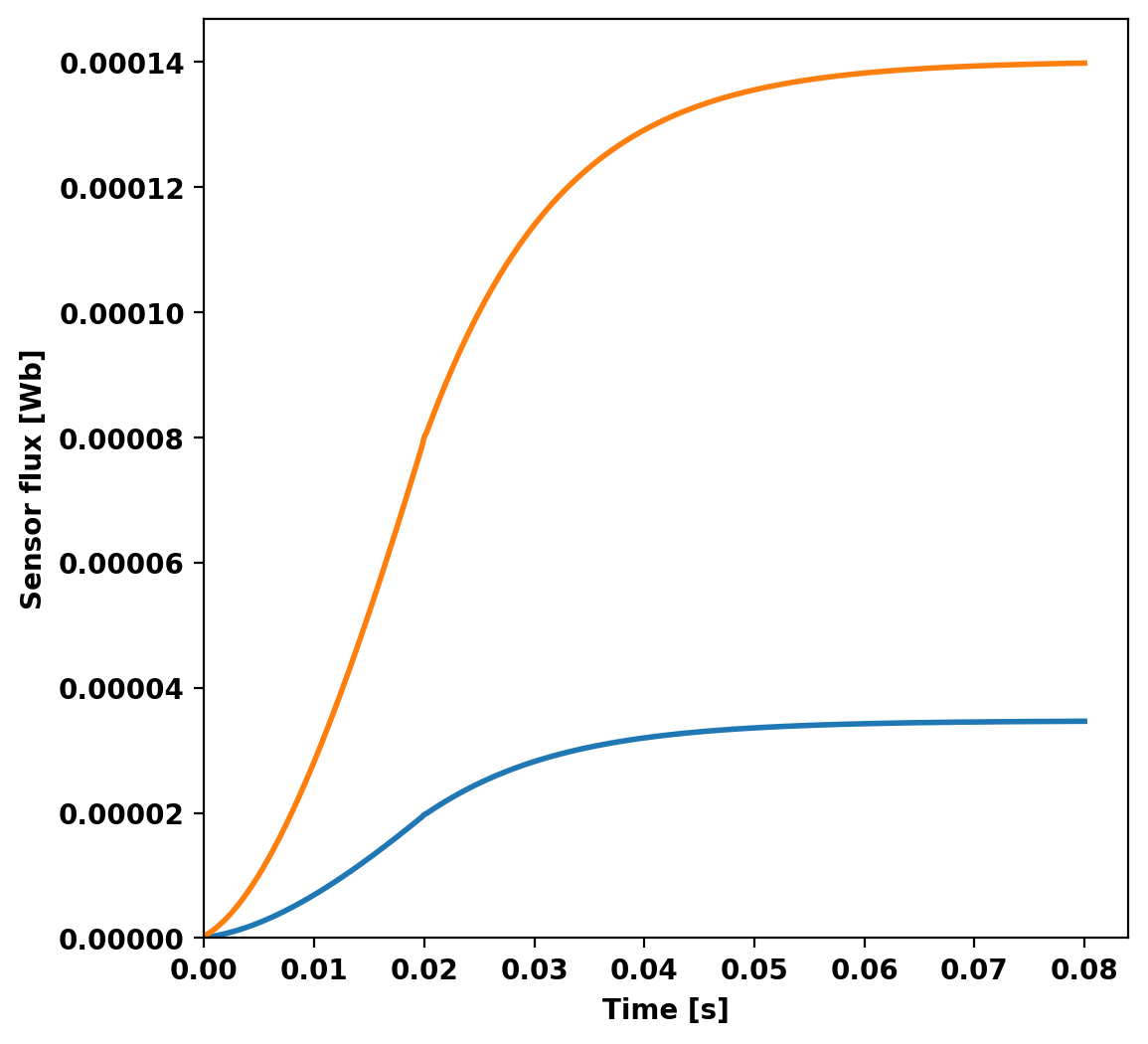
Plot sensor signals
We can now plot the signals from the two flux loops defined above as a function of time. During the time-domain run this information is stored in OFT's binary history file format, which can be read using the histfile class. This class stores the resulting signals in a Python dict-like representation.
OFT History file: floops.hist
Number of fields = 3
Number of entries = 401
Fields:
time: Simulation time [s] (d1)
Floop_1: No description (d1)
Floop_2: No description (d1)
Generate plot files
After completing the simulation we can generate plot files using tw_torus.plot_td(). Plot files are saved at a fixed timestep interval, specified by the nplot argument to run_td() with a default value of 10.
Once all fields have been saved for plotting tw_torus.build_XDMF() to generate the XDMF descriptor files for plotting with VisIt of Paraview. This method also returns a XDMF_plot_file object, which can be used to read and interact with plot data in Python (see below).
Post-processing simulation
Removing old Xdmf files
Removed 43 files
Creating output files: oft_xdmf.XXXX.h5
Found Group: thincurr
Found Mesh: icoils
# of blocks: 1
Found Mesh: smesh
# of blocks: 1
Plot current fields using pyvista
For demonstration purposes we now plot the the solution at the end of the driven phase using pyvista. We now use the plot_data object to generate a 3D plot of the current at t=2.E-2. For more information on the basic steps in this block see ThinCurr Python Example: Compute eigenstates in a plate
