In this example we show how to perform an equilibrium reconstruction in ITER from a simple with L-mode case
This example utilizes the mesh built in TokaMaker Meshing Example: Building a mesh for ITER.
- Note
- Running this example requires the h5py python package, which is installable using
pipor other standard methods.
- Warning
- The reconstruction functionality in TokaMaker is still a work in progress, as the PSI-Tri capabilities are activated and tested. Please use with care.
Load TokaMaker library
To load the TokaMaker python module we need to tell python where to the module is located. This can be done either through the PYTHONPATH environment variable or using within a script using sys.path.append() as below, where we look for the environement variable OFT_ROOTPATH to provide the path to where the OpenFUSIONToolkit is installed (/Applications/OFT on macOS).
For meshing we will use the gs_Domain class to build a 2D triangular grid suitable for Grad-Shafranov equilibria. This class uses the triangle code through a python wrapper.
Initialize TokaMaker object
We now create a OFT_env instance for execution using two threads and a TokaMaker instance to use for equilibrium calculations. Note at present only a single TokaMaker instance can be used per python kernel, so this command should only be called once in a given Jupyter notebook or python script. In the future this restriction may be relaxed.
#---------------------------------------------- Open FUSION Toolkit Initialized Development branch: v1_beta6 Revision id: 681e857 Parallelization Info: # of MPI tasks = 1 # of NUMA nodes = 1 # of OpenMP threads = 2 Fortran input file = /var/folders/52/n5qxh27n4w19qxzqygz2btbw0000gn/T/oft_64714/oftpyin XML input file = none Integer Precisions = 4 8 Float Precisions = 4 8 16 Complex Precisions = 4 8 LA backend = native #----------------------------------------------
Load mesh into TokaMaker
Now we load the mesh generated in TokaMaker Meshing Example: Building a mesh for ITER using load_gs_mesh() and setup_mesh. Then we use setup_regions(), passing the conductor and coil dictionaries for the mesh, to define the different region types. Finally, we call setup() to setup the required solver objects. During this call we can specify the desired element order (min=2, max=4) and the toroidal field through F0 = B0*R0, where B0 is the toroidal field at a reference location R0.
**** Loading OFT surface mesh
**** Generating surface grid level 1
Generating boundary domain linkage
Mesh statistics:
Area = 2.859E+02
# of points = 4757
# of edges = 14156
# of cells = 9400
# of boundary points = 112
# of boundary edges = 112
# of boundary cells = 112
Resolution statistics:
hmin = 9.924E-03
hrms = 2.826E-01
hmax = 8.466E-01
Surface grounded at vertex 870
**** Creating Lagrange FE space
Order = 2
Minlev = -1
Computing flux BC matrix
Inverting real matrix
Time = 1.0939999999999999E-003
Define a vertical stability coil
Like many elongated equilibria, the equilibrium we seek to compute below is vertically unstable. In this case we use the actual ITER Vertical Stability Coil (VSC) in order to help with convergence using the set_coil_vsc() method.
- Note
- While ITER has a "real" VSC, this is not required and this functionality can instead be used to define a "virtual" VSC by pairing coils in a way that are not necessarily paired experimentally.
Define hard limits on coil currents
Hard limits on coil currents can be set using set_coil_bounds(). In this case we just the simple and approximate bi-directional limit of 50 MA in each coil.
Bounds are specified using a dictionary of 2 element lists, containing the minimum and maximum bound, where the dictionary key corresponds to the coil names, which are available in mygs.coil_sets
Compute Equilibrium for Reconstruction
Define global quantities and targets
For the inverse case we define a target for the plasma current and the peak plasma pressure, which occurs on the magnetic axis.
- Note
- These constraints can be considered "hard" constraints, where they will be matched to good tolerance as long as the calculation converges.
Define shape targets
In order to constrain the shape of the plasma we can utilize two types of constraints:
isofluxpoints, which are points we want to lie on the same flux surface (eg. the LCFS)saddlepoints, where we want the poloidal magnetic field to vanish (eg. X-points). While one can also use this constraint to enforce a magnetic axis location, instead set_targets() should be used with argumentsR0andV0.
- Note
- These constraints can be considered "soft" constraints, where the calculation attempts to minimize error in satisfying these constraints subject to other constraints and regularization.
Here we define a handful of isoflux points that we want to lie on the LCFS of the target equilibrium. Additionally, we define a single X-point and set it as a saddle constraint as well as adding it to the list of isoflux points.
Define coil regularization matrix
In general, for a given coil set a given plasma shape cannot be exactly reproduced, which generally yields large amplitude coil currents if no constraint on the coil currents is applied. As a result, it is useful to include regularization terms for the coils to balance minimization of the shape error with the amplitude of current in the coils. In TokaMaker these regularization terms have the general form, where each term corresponds to a set of coil coefficients, target value, and weight. The coil_reg_term() method is provided to aid in defining these terms.
In this case, one regularization term is added for each coil with a single unit coefficient for that coil and target of zero with modest weights. This regularization acts to penalize the amplitude of current in each coil, acting to balance coil current with error in the shape targets. Note that the weight on the VSC virtual coil (#VSC) defined above is set high to prevent interaction with the real VS coil set (see below for further information).
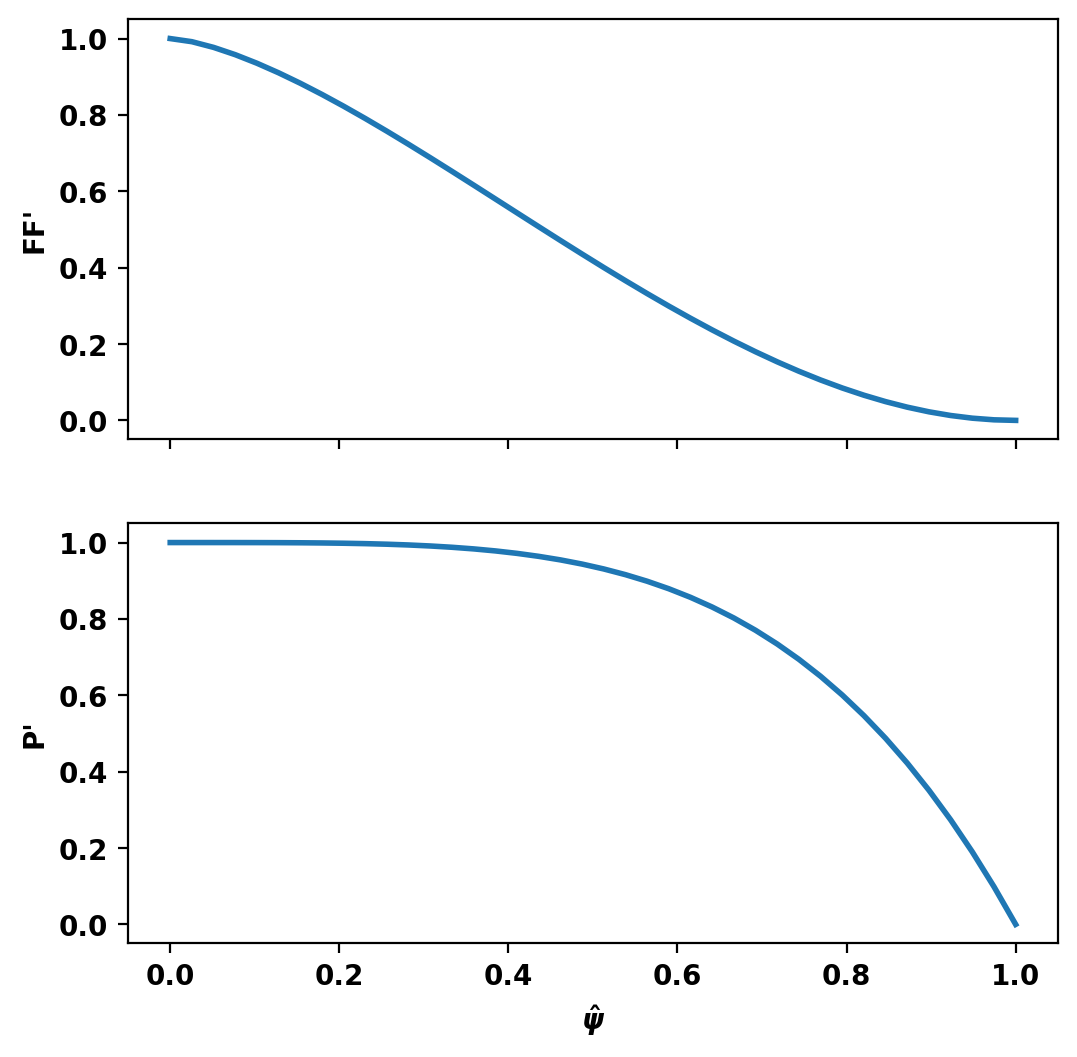
Define flux functions
Although TokaMaker has a "default" profile for the F*F' and P' terms this should almost never be used and one should instead choose an appropriate flux function for their application. In this case we use an L-mode-like profile of the form \(((1-\hat{\psi})^{\alpha})^{\gamma}\), using create_power_flux_fun(), where \(\alpha\) and \(\gamma\) are set differently for F*F' and P' to provide peaked and broad profiles respectively. Within TokaMaker this profile is represented as a piecewise linear function, which can be set up using the dictionary approach shown below.
Compute equilibrium
We can now compute a free-boundary equilibrium using these constraints. Note that before running a calculation for the first time we must initialize the flux function \(\psi\), which can be done using init_psi(). This subroutine initializes the flux using the specified Ip_target from above, which is evenly distributed over the entire plasma region or only with a boundary defined using a center point (R,Z), minor radius (a), and elongation and triangularity. Coil currents are also initialized at this point using the constraints above and this uniform plasma current initialization.
solve() is then called to compute a self-consitent Grad-Shafranov equilibrium. If the result variable (err_flag) is zero then the solution has converged to the desired tolerance ( \(10^{-6}\) by default).
Starting non-linear GS solver
1 5.7965E+00 1.5693E-01 6.4686E-01 6.4422E+00 5.3430E-01 9.8316E-04
2 1.5480E+01 9.5055E-02 2.7469E-01 6.4072E+00 5.3290E-01 1.5938E-03
3 1.9148E+01 7.9379E-02 1.2986E-01 6.3868E+00 5.3264E-01 1.6630E-03
4 2.0951E+01 7.3407E-02 6.7604E-02 6.3757E+00 5.3235E-01 1.6305E-03
5 2.1908E+01 7.0680E-02 3.6983E-02 6.3697E+00 5.3227E-01 1.5882E-03
6 2.2433E+01 6.9312E-02 2.0669E-02 6.3664E+00 5.3231E-01 1.5557E-03
7 2.2724E+01 6.8590E-02 1.1653E-02 6.3646E+00 5.3240E-01 1.5342E-03
8 2.2888E+01 6.8198E-02 6.5944E-03 6.3636E+00 5.3250E-01 1.5207E-03
9 2.2980E+01 6.7980E-02 3.7379E-03 6.3631E+00 5.3258E-01 1.5126E-03
10 2.3032E+01 6.7859E-02 2.1210E-03 6.3628E+00 5.3265E-01 1.5079E-03
11 2.3061E+01 6.7791E-02 1.2045E-03 6.3626E+00 5.3270E-01 1.5051E-03
12 2.3078E+01 6.7753E-02 6.8471E-04 6.3625E+00 5.3274E-01 1.5035E-03
13 2.3087E+01 6.7731E-02 3.8962E-04 6.3625E+00 5.3277E-01 1.5025E-03
14 2.3093E+01 6.7719E-02 2.2195E-04 6.3624E+00 5.3279E-01 1.5020E-03
15 2.3096E+01 6.7712E-02 1.2660E-04 6.3624E+00 5.3280E-01 1.5017E-03
16 2.3097E+01 6.7708E-02 7.2329E-05 6.3624E+00 5.3281E-01 1.5015E-03
17 2.3098E+01 6.7705E-02 4.1395E-05 6.3624E+00 5.3281E-01 1.5014E-03
18 2.3099E+01 6.7704E-02 2.3741E-05 6.3624E+00 5.3282E-01 1.5013E-03
19 2.3099E+01 6.7703E-02 1.3650E-05 6.3624E+00 5.3282E-01 1.5013E-03
20 2.3099E+01 6.7703E-02 7.8710E-06 6.3624E+00 5.3282E-01 1.5013E-03
21 2.3100E+01 6.7703E-02 4.5542E-06 6.3624E+00 5.3282E-01 1.5013E-03
22 2.3100E+01 6.7702E-02 2.6456E-06 6.3624E+00 5.3283E-01 1.5013E-03
23 2.3100E+01 6.7702E-02 1.5440E-06 6.3624E+00 5.3283E-01 1.5013E-03
24 2.3100E+01 6.7702E-02 9.0578E-07 6.3624E+00 5.3283E-01 1.5013E-03
Timing: 0.20457699999678880
Source: 9.0972999634686857E-002
Solve: 6.2907999963499606E-002
Boundary: 5.3660001722164452E-003
Other: 4.5330000226385891E-002
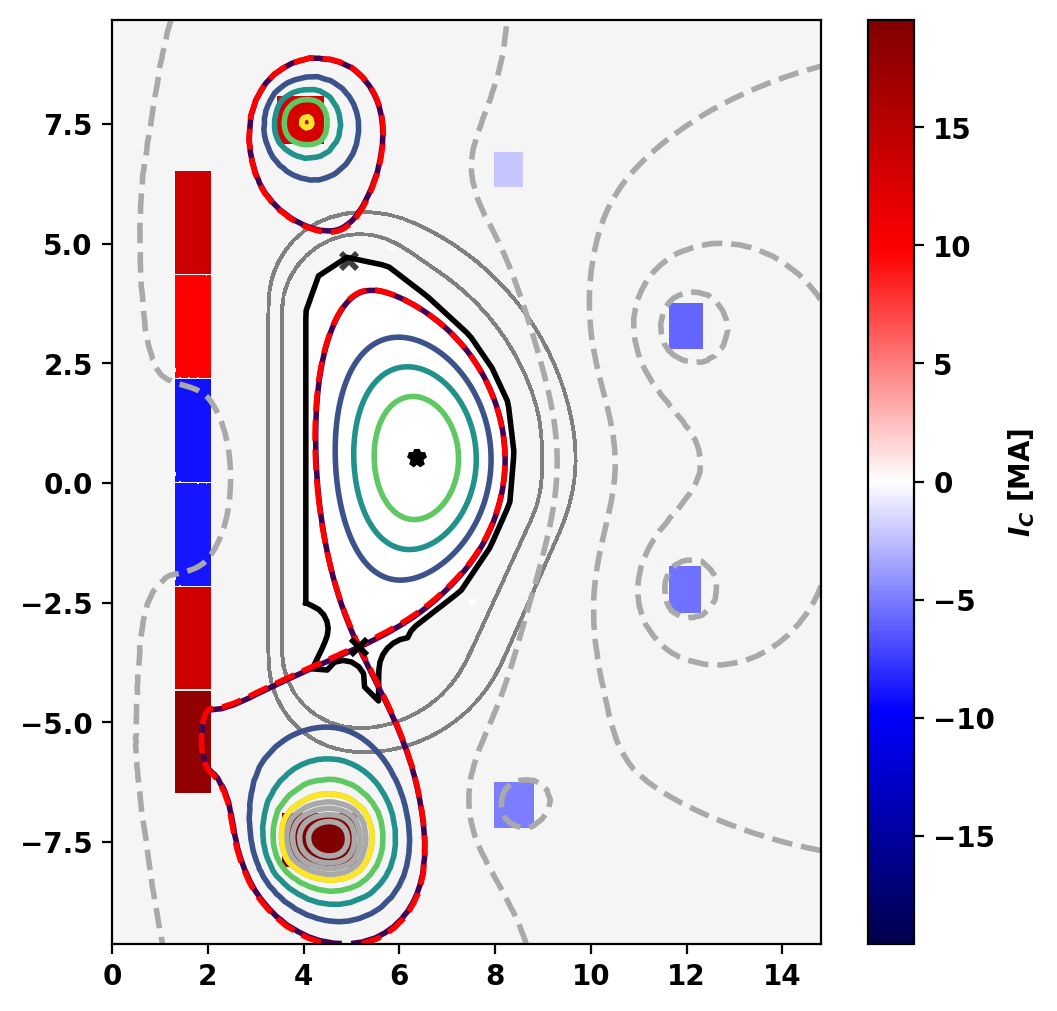
Plot equilibrium
Flux surfaces of the computed equilibrium can be plotted using the plot_psi() method. The additional plotting methods plot_machine() and plot_constraints() are also used to show context and other information. Each method has a large number of optional arguments for formatting and other options.
Print equilibrium information and coil currents
Basic parameters can be displayed using the print_info() method. For access to these quantities as variables instead the get_stats() can be used.
The final coil currents can also be retrieved using the get_coil_currents() method, which are all within the approximate coil limits imposed above.
Equilibrium Statistics: Topology = Diverted Toroidal Current [A] = 1.5600E+07 Current Centroid [m] = 6.203 0.530 Magnetic Axis [m] = 6.362 0.533 Elongation = 1.875 (U: 1.763, L: 1.987) Triangularity = 0.477 (U: 0.405, L: 0.550) Plasma Volume [m^3] = 820.079 q_0, q_95 = 0.823 2.760 Plasma Pressure [Pa] = Axis: 6.1923E+05, Peak: 6.1923E+05 Stored Energy [J] = 2.4299E+08 <Beta_pol> [%] = 42.6829 <Beta_tor> [%] = 1.7801 <Beta_n> [%] = 1.1953 Diamagnetic flux [Wb] = 1.5403E+00 Toroidal flux [Wb] = 1.2187E+02 l_i = 1.1597 Coil Currents [MA]: CS3U: 13.74 CS2U: 9.74 CS1U: -9.06 CS1L: -8.81 CS2L: 13.40 CS3L: 17.88 PF1: 12.94 PF2: -2.20 PF3: -5.95 PF4: -5.14 PF5: -5.18 PF6: 19.93 VS: 0.15
Perform Reconstruction
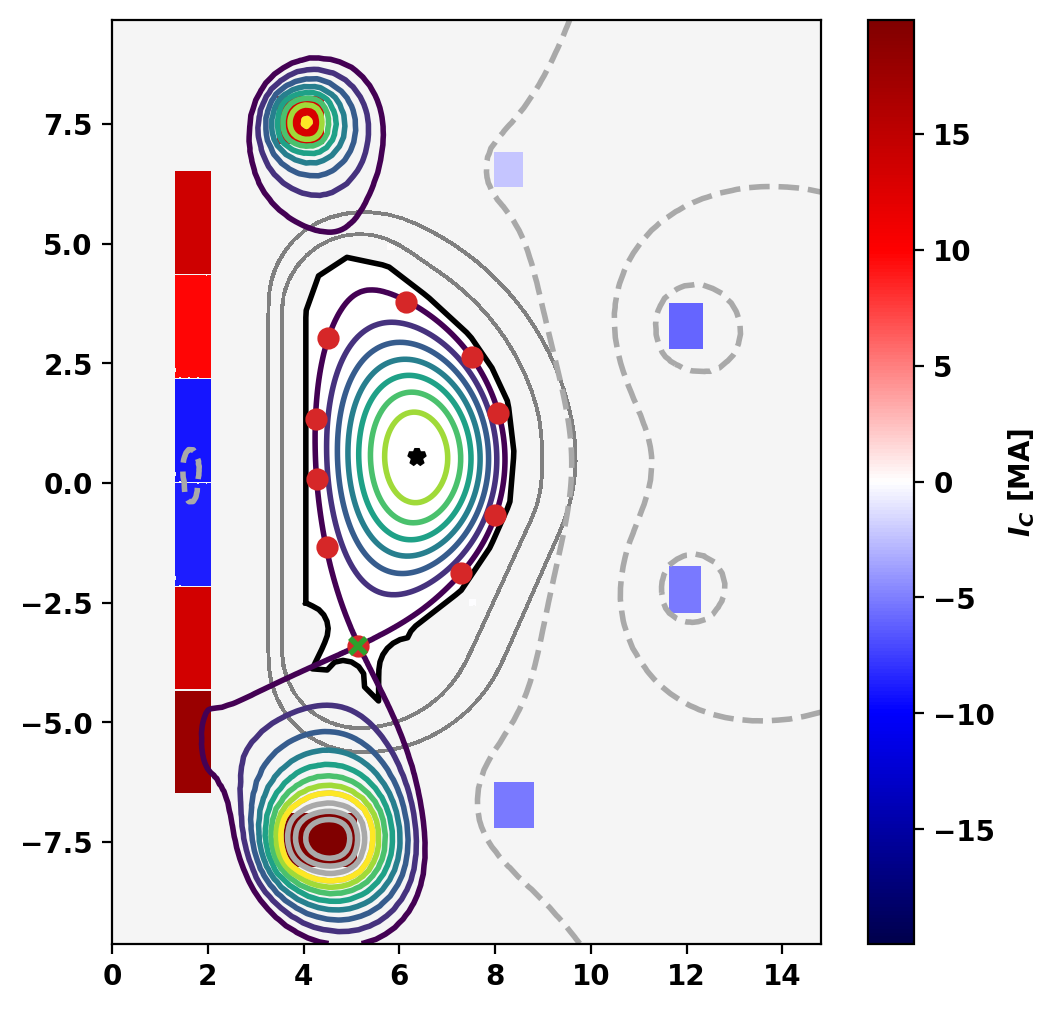
Define diagnostic set
For this example we define a simple set of flux loops and Mirnov sensors that lie on the inner vaccum vessel. The signal in these sensors will be used to constrain the reconstruction along with coil currents and global plasma quantities (eg. \(I_p\)).
Plot equilibrium and probe locations
[<matplotlib.lines.Line2D at 0x11ffe8550>]
Create reconstruction object
Set plasma current constraint
First we define a constraint on the plasma current with 5% random noise added to the signal and an appropriate error. This constraint is equivalent to the measurement of a synthetic Rigowskii coil and can be set using set_Ip().
Set flux loop constraints
Next we sample the poloidal flux at each of the locations defined above with 5% random noise added to each signal. Flux loop constraints are defined using add_flux_loop().
- Note
- Poloidal flux and \(\psi\) differ by a factor of \(2 \pi\) that must be accounted for when computing synthetic flux loop signals.
Set Mirnov constraints
Next we sample the radial and vertical magnetic field at each of the locations defined above with 5% random noise added to each signal. Local B-field constraints are defined using add_Mirnov().
Add noise to coil currents
Compute starting equilibrium
Starting non-linear GS solver
1 2.3496E+01 8.2426E-02 9.5926E-02 6.3385E+00 5.0369E-01 1.2320E-01
2 2.3331E+01 7.6491E-02 4.0608E-02 6.3461E+00 5.0101E-01 8.2651E-02
3 2.3123E+01 7.4775E-02 1.8982E-02 6.3542E+00 5.0058E-01 6.0447E-02
4 2.3039E+01 7.4161E-02 9.6013E-03 6.3607E+00 5.0131E-01 4.7738E-02
5 2.3013E+01 7.3909E-02 5.1273E-03 6.3653E+00 5.0258E-01 4.0462E-02
6 2.3007E+01 7.3788E-02 2.8748E-03 6.3684E+00 5.0406E-01 3.6243E-02
7 2.3008E+01 7.3721E-02 1.6998E-03 6.3704E+00 5.0556E-01 3.3751E-02
8 2.3008E+01 7.3678E-02 1.0753E-03 6.3717E+00 5.0700E-01 3.2238E-02
9 2.3007E+01 7.3647E-02 7.4406E-04 6.3726E+00 5.0835E-01 3.1282E-02
10 2.3005E+01 7.3623E-02 5.6856E-04 6.3731E+00 5.0960E-01 3.0647E-02
11 2.3002E+01 7.3603E-02 4.7133E-04 6.3734E+00 5.1074E-01 3.0203E-02
12 2.2999E+01 7.3586E-02 4.1117E-04 6.3736E+00 5.1179E-01 2.9874E-02
13 2.2995E+01 7.3572E-02 3.6811E-04 6.3737E+00 5.1274E-01 2.9619E-02
14 2.2992E+01 7.3559E-02 3.3337E-04 6.3737E+00 5.1361E-01 2.9413E-02
15 2.2989E+01 7.3548E-02 3.0327E-04 6.3737E+00 5.1440E-01 2.9240E-02
16 2.2985E+01 7.3537E-02 2.7628E-04 6.3737E+00 5.1512E-01 2.9092E-02
17 2.2982E+01 7.3528E-02 2.5173E-04 6.3737E+00 5.1577E-01 2.8963E-02
18 2.2980E+01 7.3520E-02 2.2931E-04 6.3737E+00 5.1637E-01 2.8850E-02
19 2.2977E+01 7.3513E-02 2.0881E-04 6.3737E+00 5.1691E-01 2.8748E-02
20 2.2975E+01 7.3506E-02 1.9008E-04 6.3737E+00 5.1740E-01 2.8657E-02
21 2.2973E+01 7.3500E-02 1.7298E-04 6.3737E+00 5.1785E-01 2.8575E-02
22 2.2971E+01 7.3494E-02 1.5738E-04 6.3736E+00 5.1825E-01 2.8502E-02
23 2.2969E+01 7.3489E-02 1.4317E-04 6.3736E+00 5.1862E-01 2.8435E-02
24 2.2968E+01 7.3485E-02 1.3022E-04 6.3736E+00 5.1896E-01 2.8374E-02
25 2.2966E+01 7.3481E-02 1.1843E-04 6.3736E+00 5.1926E-01 2.8319E-02
26 2.2965E+01 7.3477E-02 1.0771E-04 6.3736E+00 5.1954E-01 2.8269E-02
27 2.2964E+01 7.3474E-02 9.7948E-05 6.3736E+00 5.1980E-01 2.8224E-02
28 2.2962E+01 7.3471E-02 8.9069E-05 6.3735E+00 5.2003E-01 2.8183E-02
29 2.2961E+01 7.3468E-02 8.0988E-05 6.3735E+00 5.2023E-01 2.8145E-02
30 2.2961E+01 7.3465E-02 7.3640E-05 6.3735E+00 5.2042E-01 2.8111E-02
31 2.2960E+01 7.3463E-02 6.6957E-05 6.3735E+00 5.2060E-01 2.8081E-02
32 2.2959E+01 7.3461E-02 6.0879E-05 6.3735E+00 5.2075E-01 2.8053E-02
33 2.2958E+01 7.3459E-02 5.5354E-05 6.3735E+00 5.2090E-01 2.8027E-02
34 2.2958E+01 7.3457E-02 5.0329E-05 6.3735E+00 5.2103E-01 2.8004E-02
35 2.2957E+01 7.3456E-02 4.5760E-05 6.3735E+00 5.2115E-01 2.7983E-02
36 2.2957E+01 7.3454E-02 4.1604E-05 6.3735E+00 5.2125E-01 2.7964E-02
37 2.2956E+01 7.3453E-02 3.7827E-05 6.3735E+00 5.2135E-01 2.7946E-02
38 2.2956E+01 7.3452E-02 3.4393E-05 6.3735E+00 5.2144E-01 2.7931E-02
39 2.2955E+01 7.3450E-02 3.1270E-05 6.3735E+00 5.2152E-01 2.7916E-02
40 2.2955E+01 7.3450E-02 2.8431E-05 6.3735E+00 5.2159E-01 2.7903E-02
41 2.2955E+01 7.3449E-02 2.5849E-05 6.3735E+00 5.2166E-01 2.7891E-02
42 2.2954E+01 7.3448E-02 2.3502E-05 6.3734E+00 5.2172E-01 2.7880E-02
43 2.2954E+01 7.3447E-02 2.1367E-05 6.3734E+00 5.2178E-01 2.7871E-02
44 2.2954E+01 7.3446E-02 1.9427E-05 6.3734E+00 5.2183E-01 2.7862E-02
45 2.2954E+01 7.3446E-02 1.7662E-05 6.3734E+00 5.2187E-01 2.7854E-02
46 2.2953E+01 7.3445E-02 1.6058E-05 6.3734E+00 5.2191E-01 2.7846E-02
47 2.2953E+01 7.3445E-02 1.4599E-05 6.3734E+00 5.2195E-01 2.7840E-02
48 2.2953E+01 7.3444E-02 1.3272E-05 6.3734E+00 5.2198E-01 2.7833E-02
49 2.2953E+01 7.3444E-02 1.2066E-05 6.3734E+00 5.2202E-01 2.7828E-02
50 2.2953E+01 7.3443E-02 1.0970E-05 6.3734E+00 5.2204E-01 2.7823E-02
51 2.2953E+01 7.3443E-02 9.9735E-06 6.3734E+00 5.2207E-01 2.7818E-02
52 2.2953E+01 7.3443E-02 9.0674E-06 6.3734E+00 5.2209E-01 2.7814E-02
53 2.2953E+01 7.3443E-02 8.2436E-06 6.3734E+00 5.2211E-01 2.7810E-02
54 2.2952E+01 7.3442E-02 7.4946E-06 6.3734E+00 5.2213E-01 2.7807E-02
55 2.2952E+01 7.3442E-02 6.8137E-06 6.3734E+00 5.2215E-01 2.7804E-02
56 2.2952E+01 7.3442E-02 6.1946E-06 6.3734E+00 5.2217E-01 2.7801E-02
57 2.2952E+01 7.3442E-02 5.6320E-06 6.3734E+00 5.2218E-01 2.7798E-02
58 2.2952E+01 7.3441E-02 5.1204E-06 6.3734E+00 5.2220E-01 2.7796E-02
59 2.2952E+01 7.3441E-02 4.6553E-06 6.3734E+00 5.2221E-01 2.7794E-02
60 2.2952E+01 7.3441E-02 4.2324E-06 6.3734E+00 5.2222E-01 2.7792E-02
61 2.2952E+01 7.3441E-02 3.8480E-06 6.3734E+00 5.2223E-01 2.7790E-02
62 2.2952E+01 7.3441E-02 3.4984E-06 6.3734E+00 5.2224E-01 2.7789E-02
63 2.2952E+01 7.3441E-02 3.1806E-06 6.3734E+00 5.2225E-01 2.7787E-02
64 2.2952E+01 7.3441E-02 2.8917E-06 6.3734E+00 5.2225E-01 2.7786E-02
65 2.2952E+01 7.3441E-02 2.6290E-06 6.3734E+00 5.2226E-01 2.7785E-02
66 2.2952E+01 7.3440E-02 2.3902E-06 6.3734E+00 5.2227E-01 2.7783E-02
67 2.2952E+01 7.3440E-02 2.1731E-06 6.3734E+00 5.2227E-01 2.7782E-02
68 2.2952E+01 7.3440E-02 1.9757E-06 6.3734E+00 5.2228E-01 2.7782E-02
69 2.2952E+01 7.3440E-02 1.7962E-06 6.3734E+00 5.2228E-01 2.7781E-02
70 2.2952E+01 7.3440E-02 1.6331E-06 6.3734E+00 5.2229E-01 2.7780E-02
71 2.2952E+01 7.3440E-02 1.4848E-06 6.3734E+00 5.2229E-01 2.7779E-02
72 2.2952E+01 7.3440E-02 1.3500E-06 6.3734E+00 5.2229E-01 2.7779E-02
73 2.2952E+01 7.3440E-02 1.2274E-06 6.3734E+00 5.2230E-01 2.7778E-02
74 2.2952E+01 7.3440E-02 1.1159E-06 6.3734E+00 5.2230E-01 2.7778E-02
75 2.2952E+01 7.3440E-02 1.0146E-06 6.3734E+00 5.2230E-01 2.7777E-02
76 2.2952E+01 7.3440E-02 9.2243E-07 6.3734E+00 5.2230E-01 2.7777E-02
Timing: 0.65570299996761605
Source: 0.28560899972217157
Solve: 0.20822999981464818
Boundary: 1.7690999957267195E-002
Other: 0.14417300047352910
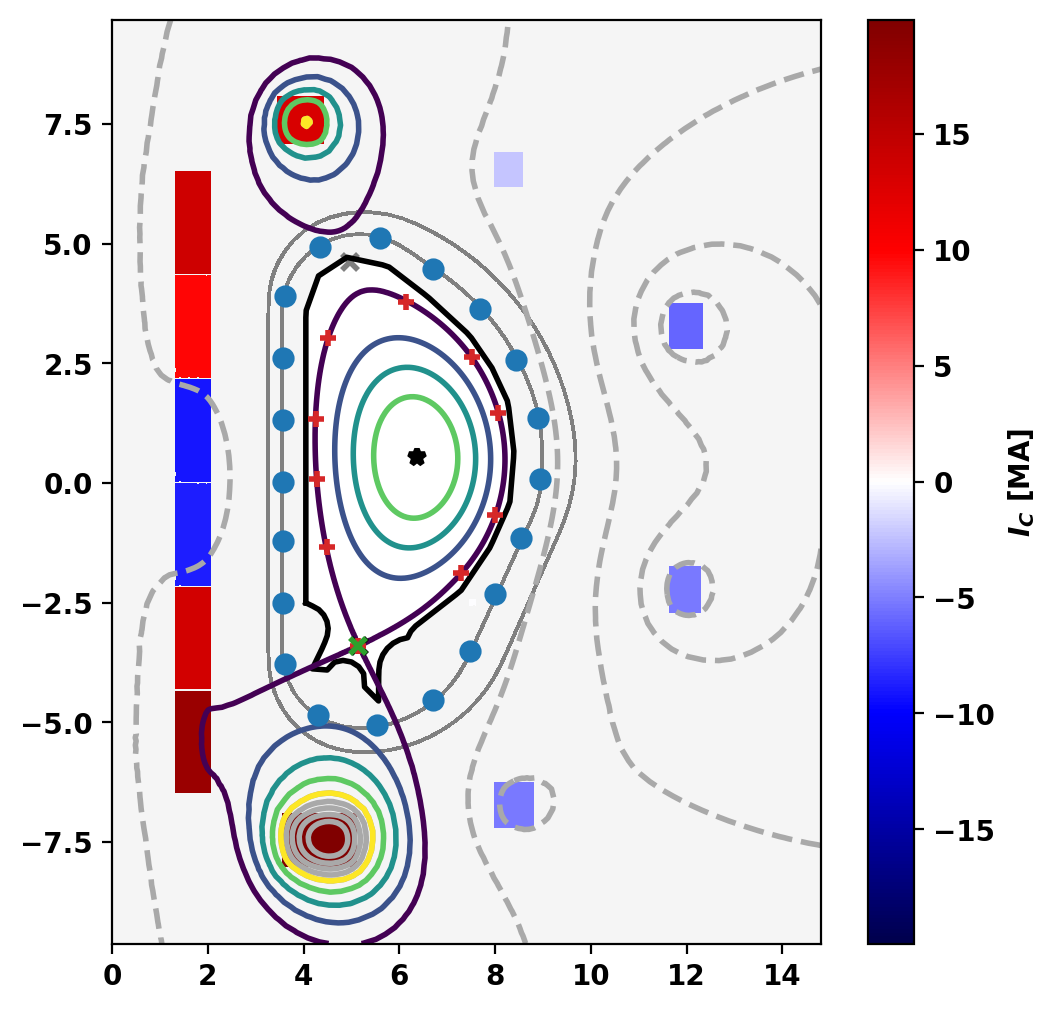
Plot starting equilibrium
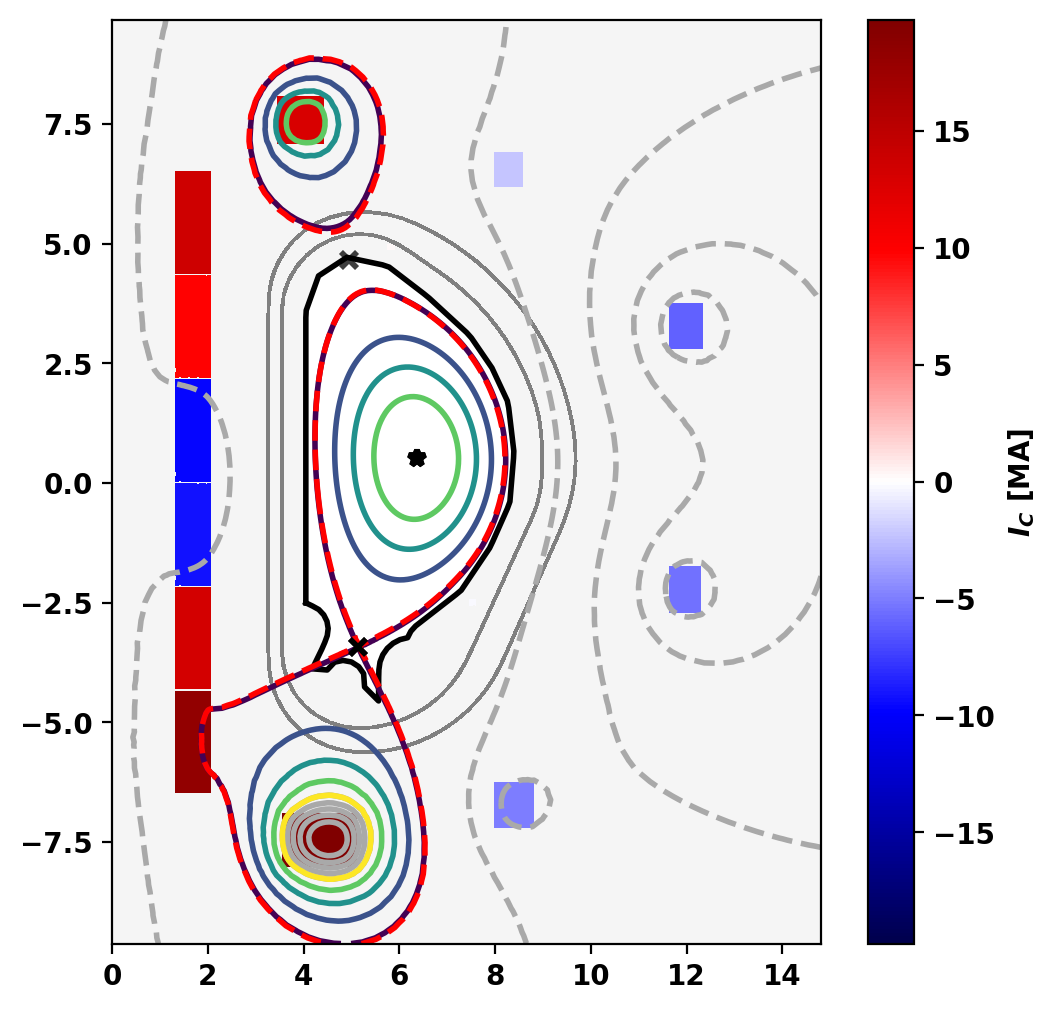
Perform reconstruction
*** Loading fit constraints *** ======================================== Starting Fit: # of free parameters = 15 # of constraints = 74 Function evaluation 1 Alam = 2.295E+01 P_scale = 7.344E-02 R0_target = 6.373E+00 V0_target = 5.223E-01 Coil currents [%] = 0.000E+00 0.000E+00 -0.000E+00 -0.000E+00 0.000E+00 0.000E+00 0.000E+00 -0.000E+00 -0.000E+00 -0.000E+00 -0.000E+00 0.000E+00 0.000E+00 Maximum Rel Error = 2.544E-01 Maximum Abs Error = 1.362E+01 Total Weighted Error = 7.460E+00 RMS Weighted Error = 8.672E-01 Function evaluation 2 Alam = 2.295E+01 P_scale = 7.344E-02 R0_target = 6.373E+00 V0_target = 5.223E-01 Coil currents [%] = 0.000E+00 0.000E+00 -0.000E+00 -0.000E+00 0.000E+00 0.000E+00 0.000E+00 -0.000E+00 -0.000E+00 -0.000E+00 -0.000E+00 0.000E+00 0.000E+00 Maximum Rel Error = 2.544E-01 Maximum Abs Error = 1.361E+01 Total Weighted Error = 7.460E+00 RMS Weighted Error = 8.672E-01 Gradient evaluation 1 Function evaluation 3 Alam = 2.174E+01 P_scale = 7.627E-02 R0_target = 6.377E+00 V0_target = 5.223E-01 Coil currents [%] = -6.417E-03 1.016E-02 -5.304E-02 -1.945E-02 1.359E-02 -1.548E-02 5.578E-03 -2.241E-02 -2.264E-02 -1.151E-02 -2.418E-02 -1.043E-02 -2.289E-09 Maximum Rel Error = 5.304E-02 Maximum Abs Error = 5.110E+05 Total Weighted Error = 3.783E+00 RMS Weighted Error = 4.397E-01 Gradient evaluation 2 Function evaluation 4 Alam = 2.172E+01 P_scale = 7.634E-02 R0_target = 6.377E+00 V0_target = 5.223E-01 Coil currents [%] = -6.340E-03 1.001E-02 -5.342E-02 -1.938E-02 1.336E-02 -1.524E-02 5.586E-03 -2.221E-02 -2.293E-02 -1.143E-02 -2.426E-02 -1.046E-02 -8.252E-06 Maximum Rel Error = 5.342E-02 Maximum Abs Error = 5.147E+05 Total Weighted Error = 3.782E+00 RMS Weighted Error = 4.397E-01 ======================================== Fit Complete Final error = 3.782E+00 Termination reason: Actual and predicted delta_rel(err) < ftol Alam = 2.172E+01 P_scale = 7.634E-02 R0_target = 6.377E+00 V0_target = 5.223E-01 Coil currents [%] = -6.340E-03 1.001E-02 -5.342E-02 -1.938E-02 1.336E-02 -1.524E-02 5.586E-03 -2.221E-02 -2.293E-02 -1.143E-02 -2.426E-02 -1.046E-02 -8.252E-06 Maximum Rel Error = 5.342E-02 Maximum Abs Error = 5.147E+05 Total Weighted Error = 3.782E+00 RMS Weighted Error = 4.397E-01
Print equilibrium information and coil currents
As above we use print_info() and get_coil_currents() to display information on the final equilibrium.
Equilibrium Statistics: Topology = Diverted Toroidal Current [A] = 1.5733E+07 Current Centroid [m] = 6.216 0.517 Magnetic Axis [m] = 6.377 0.522 Elongation = 1.889 (U: 1.768, L: 2.009) Triangularity = 0.472 (U: 0.405, L: 0.539) Plasma Volume [m^3] = 822.871 q_0, q_95 = 0.840 2.757 Plasma Pressure [Pa] = Axis: 6.9104E+05, Peak: 6.9104E+05 Stored Energy [J] = 2.7467E+08 <Beta_pol> [%] = 47.5304 <Beta_tor> [%] = 2.0102 <Beta_n> [%] = 1.3337 Diamagnetic flux [Wb] = 1.4520E+00 Toroidal flux [Wb] = 1.2189E+02 l_i = 1.1327 Coil Currents [MA]: CS3U: 13.64 CS2U: 9.89 CS1U: -9.12 CS1L: -8.94 CS2L: 13.36 CS3L: 17.97 PF1: 12.95 PF2: -2.23 PF3: -5.92 PF4: -5.35 PF5: -4.97 PF6: 19.56 VS: 0.15
Plot final reconstructed equilibrium