In this example we show how to generate a mesh for the CUTE device using TokaMaker's built in mesh generation.

Note: Running this example requires the h5py python packages, which is installable using pip or other standard methods.

import os
import sys
import json
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = "retina"

Load TokaMaker library

To load the TokaMaker python module we need to tell python where to the module is located. This can be done either through the PYTHONPATH environment variable or using within a script using sys.path.append() as below, where we look for the environement variable OFT_ROOTPATH to provide the path to where the OpenFUSIONToolkit is installed (/Applications/OFT on macOS).

For meshing we will use the gs_Domain class to build a 2D triangular grid suitable for Grad-Shafranov equilibria. This class uses the triangle code through a simple internal python wrapper within OFT.

tokamaker_python_path = os.getenv('OFT_ROOTPATH')
if tokamaker_python_path is not None:
    sys.path.append(os.path.join(tokamaker_python_path,'python'))
from OpenFUSIONToolkit.TokaMaker import TokaMaker
from OpenFUSIONToolkit.TokaMaker.meshing import save_gs_mesh, gs_Domain

Build mesh

Set mesh resolution for each region

First we define some target sizes to set the resolution in out grid. These variables will be used later and represent the target edge size within a given region, where units are in meters. In this case we are using a fairly fine resolution of 1 cm in the plasma region, to provide accuracy for the time-dependen simulations performed in TokaMaker Example: Vertical stability in CUTE for different elongations, and a coarse resolution of 5 cm in the vacuum region.

Note: When setting up a new machine these values will need to scale with the overall size of the device/domain. Additionally, one should perform a convergence study, by increasing resolution (decreasing target size) by at least a factor of two in all regions to ensure the results are not sensitive to your choice of grid size.

plasma_resolution = 0.01
coil_resolution = 0.02
vv_resolution = 0.02
vac_resolution = 0.05

Load geometry information

The geometry information (eg. bounding curves for vacuum vessels) are now loaded from a JSON file. For simple geometries, testing, or generative usage this can be created directly in the code. However, it is often helpful to separate this information into a fixed datafile as here. This JSON file contains the following:

vv: Two contours of R,Z points defining the inner and outer surface of the vacuum vessel
coils: A dictionary of values defining the E and F coils in the poloidal cross-section

Note: For CUTE the limiter is the inner surface of the VV.

with open('CUTE_geom.json','r') as fid:

CUTE_geom = json.load(fid)

Define regions and attributes

We now create and define the various logical mesh regions. In the CUTE case we have 4 region groups:

air: The region outside the vacuum vessel
plasma: The region inside the limiter (vacuum vessel) where the plasma will exist
vv: The vacuum vessel
PF1,...: Each of the 28 coil sets in CUTE (14 CS coils, 14 PF coils)

For each region you can provide a target size and one of four region types:

plasma: The region where the plasma can exist and the classic Grad-Shafranov equation with \(F*F'\) and \(P'\) are allowed. There can only be one region of this type
vacuum: A region where no current can flow and \(\nabla^* \psi = 0\) is solved
boundary: A special case of the vacuum region, which forms the outer boundary of the computational domain. A region of this type is required if more than one region is specified
conductor: A region where toroidal current can flow passively (no externally applied voltage). For this type of region the resistivity should be specified with the argument eta in units of \(\omega \mathrm{-m}\).
coil: A region where toroidal current can flow with specified amplitude through set_coil_currents() or via shape optimization set_coil_reg() and set_isoflux()

# Create a G-S domain
gs_mesh = gs_Domain()
# Define region information for mesh
gs_mesh.define_region('air',vac_resolution,'boundary')              # Define the bounding region
gs_mesh.define_region('plasma',plasma_resolution,'plasma')          # Define the plasma region and resolution
gs_mesh.define_region('vv',vv_resolution,'conductor',eta=1.26E-5)   # Define the VV itself
# Define each of the PF coils
for key, coil in CUTE_geom['coils'].items():
    gs_mesh.define_region(key,coil_resolution,'coil',nTurns=coil['nturns'])

Define geometry for region boundaries

Once the region types and properties are defined we now define the geometry of the mesh using shapes and references to the defined regions.

We add the vacuum vessel as an "annulus" with curves defining the inner and outer edges respectively. We also reference plasma as the region enclosed by the annulus, vv as the annular region itself, and air as the region outside the annulus.
We add each of the 28 CS/PF coils as "rectangles", which are defined by a center point (R,Z) along with a width (W) and height (H). We also reference air as the region outside each coil.

# Define geometry
gs_mesh.add_annulus(CUTE_geom['vv']['inner_contour'],'plasma',CUTE_geom['vv']['outer_contour'],'vv',parent_name='air')  # Define the shape of the VV
# Define the shape of the PF coils
for key, coil in CUTE_geom['coils'].items():
    gs_mesh.add_rectangle(coil['rc'],coil['zc'],coil['w'],coil['h'],key,parent_name='air')

Plot topology

After defining the logical and physical topology we can now plot the curves within the definitions to double check everything is in the right place.

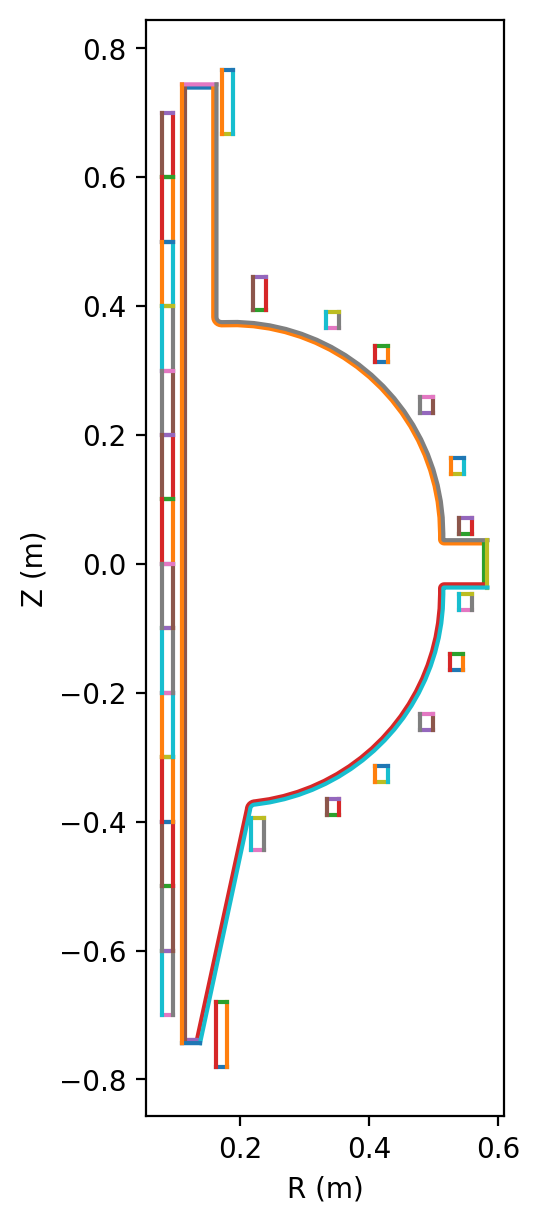
fig, ax = plt.subplots(1,1,figsize=(4,6),constrained_layout=True)

gs_mesh.plot_topology(fig,ax)

Create mesh

Now we generate the actual mesh using the build_mesh() method. Additionally, if coil and/or conductor regions are defined the get_coils() and get_conductors() methods should also be called to get descriptive dictionaries for later use in TokaMaker. This step may take a few moments as triangle generates the mesh.

Note that, as is common with unstructured meshes, the mesh is stored a list of points mesh_pts of size (np,2), a list of cells formed from three points each mesh_lc of size (nc,3), and an array providing a region id number for each cell mesh_reg of size (nc,), which is mapped to the names above using the coil_dict and cond_dict dictionaries.

mesh_pts, mesh_lc, mesh_reg = gs_mesh.build_mesh()
coil_dict = gs_mesh.get_coils()
cond_dict = gs_mesh.get_conductors()

Assembling regions:
  # of unique points    = 829
  # of unique segments  = 115
Generating mesh:
  # of points  = 5796
  # of cells   = 11488
  # of regions = 31

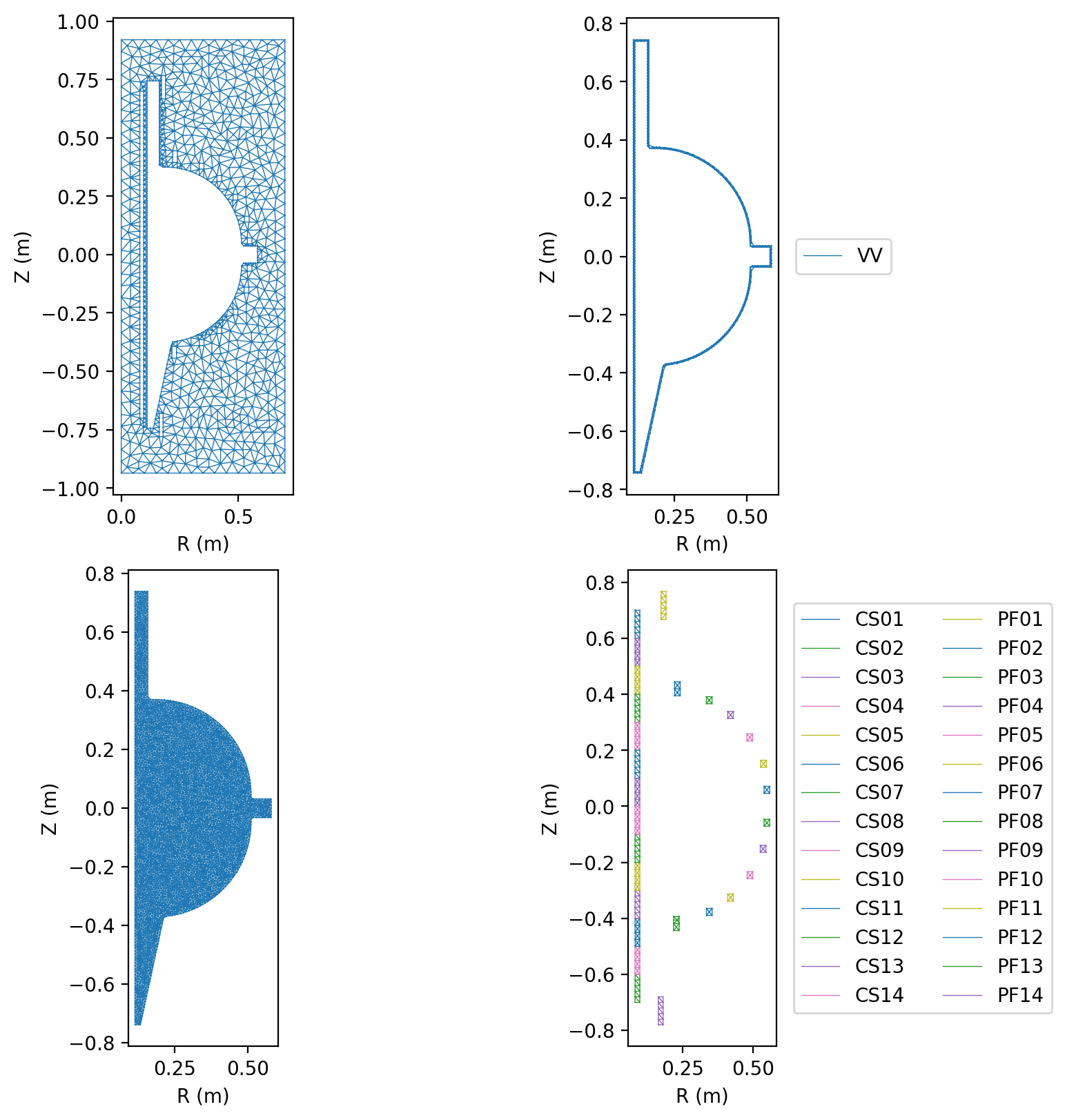
Plot resulting regions and grid

We now plot the mesh by region to inspect proper generation.

fig, ax = plt.subplots(2,2,figsize=(8,8),constrained_layout=True)

gs_mesh.plot_mesh(fig,ax)

Save mesh for later use

As generation of the mesh often takes comparable, or longer, time compare to runs in TokaMaker it is useful to separate generation of the mesh into a different script as demonstrated here. The method save_gs_mesh() can be used to save the resulting information for later use. This is done using and an HDF5 file through the h5py library.

save_gs_mesh(mesh_pts,mesh_lc,mesh_reg,coil_dict,cond_dict,'CUTE_mesh.h5')